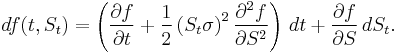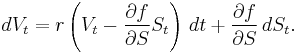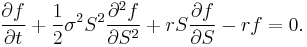Itō's lemma
In mathematics, Itō's lemma is used in Itō stochastic calculus to find the differential of a function of a particular type of stochastic process. It is named after its discoverer, Kiyoshi Itō. It is the stochastic calculus counterpart of the chain rule in ordinary calculus and is best memorized using the Taylor series expansion and retaining the second order term related to the stochastic component change. The lemma is widely employed in mathematical finance and its best known application is in the derivation of the Black–Scholes equation used to value options. Ito's Lemma is also referred to currently as the Itō–Doeblin Theorem in recognition of the recently discovered work of Wolfgang Doeblin.[1]
Contents |
Mathematical formulation of Itō's lemma
In the following subsections we discuss versions of Itō's lemma for different types of stochastic processes.
Itō drift-diffusion processes
In its simplest form, Itō's lemma states the following: for an Itō drift-diffusion process
and any twice differentiable function ƒ(t, x) of two real variables t and x, one has
This immediately implies that ƒ(t, X) is itself an Itō drift-diffusion process.
In higher dimensions, Ito's lemma states
where 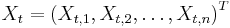 is a vector of Itō processes,
is a vector of Itō processes, 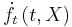 is the partial differential w.r.t. t,
is the partial differential w.r.t. t, 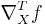 is the gradient of ƒ w.r.t. X, and
is the gradient of ƒ w.r.t. X, and 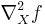 is the Hessian matrix of ƒ w.r.t. X.
is the Hessian matrix of ƒ w.r.t. X.
Continuous semimartingales
More generally, the above formula also holds for any continuous d-dimensional semimartingale X = (X1,X2,…,Xd), and twice continuously differentiable and real valued function f on Rd. Some people prefer to present the formula in another form with cross variation shown explicitly as follows, f(X) is a semimartingale satisfying
In this expression, the term fi represents the partial derivative of f(x) with respect to xi, and [Xi,Xj ] is the quadratic covariation process of Xi and Xj.
Poisson jump processes
We may also define functions on discontinuous stochastic processes.
Let h be the jump intensity. The Poisson process model for jumps is that the probability of one jump in the interval ![[t, t %2B \Delta t]](/2012-wikipedia_en_all_nopic_01_2012/I/e9ceeb8058726ba0a6fb37e1363a2cb3.png) is
is  plus higher order terms. h could be a constant, a deterministic function of time, or a stochastic process. The survival probability
plus higher order terms. h could be a constant, a deterministic function of time, or a stochastic process. The survival probability 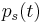 is the probability that no jump has occurred in the interval
is the probability that no jump has occurred in the interval ![[0,t]](/2012-wikipedia_en_all_nopic_01_2012/I/21b8fce671acf5fa4690193ad7ef3461.png) . The change in the survival probability is
. The change in the survival probability is
So
Let 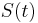 be a discontinuous stochastic process. Write
be a discontinuous stochastic process. Write 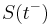 for the value of S as we approach t from the left. Write
for the value of S as we approach t from the left. Write 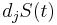 for the non-infinitesimal change in
for the non-infinitesimal change in 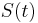 as a result of a jump. Then
as a result of a jump. Then
Let z be the magnitude of the jump and let 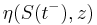 be the distribution of z. The expected magnitude of the jump is
be the distribution of z. The expected magnitude of the jump is
Define 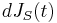 , a compensated process and martingale, as
, a compensated process and martingale, as
Then
Consider a function 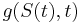 of jump process
of jump process 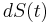 . If
. If 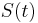 jumps by
jumps by 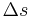 then
then 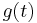 jumps by
jumps by 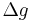 .
. 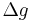 is drawn from distribution
is drawn from distribution 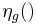 which may depend on
which may depend on 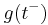 , dg and
, dg and 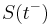 . The jump part of
. The jump part of  is
is
If  contains drift, diffusion and jump parts, then Itō's Lemma for
contains drift, diffusion and jump parts, then Itō's Lemma for 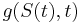 is
is
Itō's lemma for a process which is the sum of a drift-diffusion process and a jump process is just the sum of the Itō's lemma for the individual parts.
Non-continuous semimartingales
Itō's lemma can also be applied to general d-dimensional semimartingales, which need not be continuous. In general, a semimartingale is a càdlàg process, and an additional term needs to be added to the formula to ensure that the jumps of the process are correctly given by Itō's lemma. For any cadlag process Yt, the left limit in t is denoted by Yt-, which is a left-continuous process. The jumps are written as ΔYt = Yt - Yt-. Then, Itō's lemma states that if X = (X1,X2,…,Xd) is a d-dimensional semimartingale and f is a twice continuously differentiable real valued function on Rd then f(X) is a semimartingale, and
This differs from the formula for continuous semimartingales by the additional term summing over the jumps of X, which ensures that the jump of the right hand side at time t is Δf(Xt).
Informal derivation
A formal proof of the lemma requires us to take the limit of a sequence of random variables, which is not done here. Instead, we give a sketch of how one can derive Itō's lemma by expanding a Taylor series and applying the rules of stochastic calculus.
Assume the Itō process is in the form of
Expanding f(x, t) in a Taylor series in x and t we have
and substituting a dt + b dB for dx gives
In the limit as dt tends to 0, the dt2 and dt dB terms disappear but the dB2 term tends to dt. The latter can be shown if we prove that
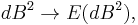 since
since 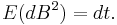
Deleting the dt2 and dt dB terms, substituting dt for dB2, and collecting the dt and dB terms, we obtain
as required.
The formal proof is somewhat technical and is beyond the current state of this article.
Examples
Geometric Brownian motion
A process S is said to follow a geometric Brownian motion with volatility σ and drift μ if it satisfies the stochastic differential equation dS = S(σdB + μdt), for a Brownian motion B. Applying Itō's lemma with f(S) = log(S) gives
It follows that log(St) = log(S0) + σBt + (μ − σ2/2)t, and exponentiating gives the expression for S,
The Doléans exponential
The Doléans exponential (or stochastic exponential) of a continuous semimartingale X can be defined as the solution to the SDE dY = Y dX with initial condition Y0 = 1. It is sometimes denoted by Ɛ(X). Applying Itō's lemma with f(Y) = log(Y) gives
Exponentiating gives the solution
Black–Scholes formula
Itō's lemma can be used to derive the Black–Scholes formula for an option. Suppose a stock price follows a Geometric Brownian motion given by the stochastic differential equation dS = S(σdB + μ dt). Then, if the value of an option at time t is f(t,St), Itō's lemma gives
The term (∂f/∂S) dS represents the change in value in time dt of the trading strategy consisting of holding an amount ∂f/∂S of the stock. If this trading strategy is followed, and any cash held is assumed to grow at the risk free rate r, then the total value V of this portfolio satisfies the SDE
This strategy replicates the option if V = f(t,S). Combining these equations gives the celebrated Black-Scholes equation
See also
Notes
References
- Kiyoshi Itō (1951). On stochastic differential equations. Memoirs, American Mathematical Society 4, 1–51.
- Hagen Kleinert (2004). Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 4th edition, World Scientific (Singapore); Paperback ISBN 981-238-107-4. Also available online: PDF-files. This textbook also derives generalizations of Itō's lemma for non-Wiener (non-Gaussian) processes.
- Bernt Øksendal (2000). Stochastic Differential Equations. An Introduction with Applications, 5th edition, corrected 2nd printing. Springer. ISBN 3-540-63720-6. Sections 4.1 and 4.2.
- Domingo Tavella (2002). Quantitative Methods in Derivatives Pricing: An Introduction to Computational Finance, John Wiley and Sons. ISBN 9780471274797. Pages 36–39.
External links
- Derivation, Prof. Thayer Watkins
- Informal proof, optiontutor
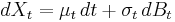
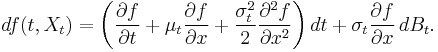
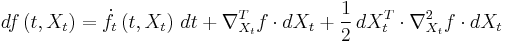
![df(X_t) = \sum_{i=1}^d f_{i}(X_t)\,dX^i_t %2B \frac{1}{2}\sum_{i,j=1}^df_{i,j}(X_t)\,d[X^i,X^j]_t.](/2012-wikipedia_en_all_nopic_01_2012/I/eedd1abfa1030a124a5422ad0330147b.png)
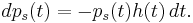
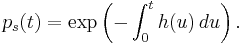
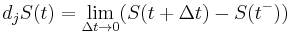
![E[d_j S(t)]=h(S(t^-)) \, dt \int_z z \eta(S(t^-),z) \, dz.](/2012-wikipedia_en_all_nopic_01_2012/I/5b47218f993a92235bff4d525e93a5c4.png)
![d J_S(t)=d_j S(t)-E[d_j S(t)]=S(t)-S(t^-)-(h(S(t^-)) \int_z z \eta(S(t^-),z) \, dz) \, dt.](/2012-wikipedia_en_all_nopic_01_2012/I/f071381d93765b133bce3ffcff3ca5c0.png)
![d_j S(t) = E[d_j S(t)] %2B d J_S(t) = h(S(t^-)) (\int_z z \eta(S(t^-),z) \, dz) dt %2B d J_S(t).](/2012-wikipedia_en_all_nopic_01_2012/I/3ecfaf6d2b130e2df065a258fa353922.png)
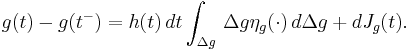
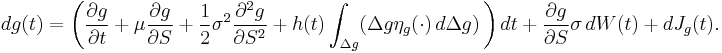
![\begin{align}
f(X_t)= & f(X_0)%2B\sum_{i=1}^d\int_0^t f_{i}(X_{s-})\,dX^i_s %2B \frac{1}{2}\sum_{i,j=1}^d \int_0^t f_{i,j}(X_{s-})\,d[X^i,X^j]_s\\
&{} %2B \sum_{s\le t}\left(\Delta f(X_s)-\sum_{i=1}^df_{i}(X_{s-})\,\Delta X^i_s-\frac{1}{2}\sum_{i,j=1}^d f_{i,j}(X_{s-})\,\Delta X^i_s \, \Delta X^j_s\right).
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/60657d8d61bf186d9053680a9bc98664.png)
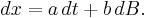
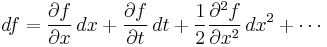
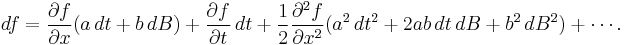
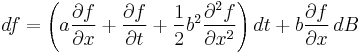
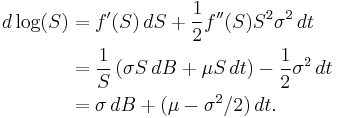
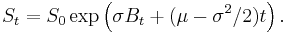
![\begin{align}
d\log(Y) &= \frac{1}{Y}\,dY -\frac{1}{2Y^2}\,d[Y] \\
&= dX - \frac{1}{2}\,d[X].
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/5d2647440500120747e527b8198862cd.png)
![Y_t = \exp\left(X_t-X_0-[X]_t/2\right).](/2012-wikipedia_en_all_nopic_01_2012/I/40513bcdb0aaa26d4ee74f592106aa71.png)